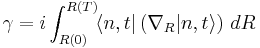Geometric phase
In classical and quantum mechanics, the geometric phase, Pancharatnam–Berry phase (named after S. Pancharatnam and Sir Michael Berry), Pancharatnam phase or most commonly Berry phase, is a phase acquired over the course of a cycle, when the system is subjected to cyclic adiabatic processes, which results from the geometrical properties of the parameter space of the Hamiltonian. The phenomenon was first discovered in 1956,[1] and rediscovered in 1984.[2] It can be seen in the Aharonov–Bohm effect and in the conical intersection of potential energy surfaces. In the case of the Aharonov–Bohm effect, the adiabatic parameter is the magnetic field inside the solenoid, and cyclic means that the difference involved in measuring the effect by interference corresponds to a closed loop, in the usual way (see below). In the case of the conical intersection, the adiabatic parameters are the molecular coordinates. Apart from quantum mechanics, it arises in a variety of other wave systems, such as classical optics. As a rule of thumb, it occurs whenever there are at least two parameters affecting a wave, in the vicinity of some sort of singularity or some sort of hole in the topology.
Waves are characterized by amplitude and phase, and both may vary as a function of those parameters. The Berry phase occurs when both parameters are changed simultaneously but very slowly (adiabatically), and eventually brought back to the initial configuration. In quantum mechanics, this could e.g. involve rotations but also translations of particles, which are apparently undone at the end. Intuitively one expects that the waves in the system return to the initial state, as characterized by the amplitudes and phases (and accounting for the passage of time). However, if the parameter excursions correspond to a cyclic loop instead of a self-retracing back-and-forth variation, then it is possible that the initial and final states differ in their phases. This phase difference is the Berry phase, and its occurrence typically indicates that the system's parameter dependence is singular (undefined) for some combination of parameters.
To measure the Berry phase in a wave system, an interference experiment is required. The Foucault pendulum is an example from classical mechanics that is sometimes used to illustrate the Berry phase. This mechanics analogue of the Berry phase is known as the Hannay angle.
Contents |
Theory
In general the geometric phase is given by:
Examples of geometric phases
The Foucault pendulum
One of the easiest examples is the Foucault pendulum. An easy explanation in terms of geometric phases is given by von Bergmann and von Bergmann:[3]
- How does the pendulum precess when it is taken around a general path C? For transport along the equator, the pendulum will not precess. [...] Now if C is made up of geodesic segments, the precession will all come from the angles where the segments of the geodesics meet; the total precession is equal to the net deficit angle which in turn equals the solid angle enclosed by C modulo 2π. Finally, we can approximate any loop by a sequence of geodesic segments, so the most general result (on or off the surface of the sphere) is that the net precession is equal to the enclosed solid angle.
In summary, there are no inertial forces that could make the pendulum precess. Thus the orientation of the pendulum undergoes parallel transport along the path of fixed latitude. By the Gauss–Bonnet theorem the phase shift is given by the enclosed solid angle.
Polarized light in an optical fiber
A second example is linearly polarized light entering a single-mode optical fiber. Suppose the fiber traces out some path in space and the light exits the fiber in the same direction as it entered. Then compare the initial and final polarizations. In semiclassical approximation the fiber functions as a waveguide and the momentum of the light is at all times tangent to the fiber. The polarization can be thought of as an orientation perpendicular to the momentum. As the fiber traces out its path, the momentum vector of the light traces out a path on the sphere in momentum space. The path is closed since initial and final directions of the light coincide, and the polarization is a vector tangent to the sphere. Going to momentum space is equivalent to taking the Gauss map. There are no forces that could make the polarization turn, just the constraint to remain tangent to the sphere. Thus the polarization undergoes parallel transport and the phase shift is given by the enclosed solid angle (times the spin, which in case of light is 1).
Stochastic pump effect
A stochastic pump is a classical stochastic system that responds with nonzero, on average, currents to periodic changes of parameters. The stochastic pump effect can be interpreted in terms of a geometric phase in evolution of the moment generating function of stochastic currents.[4]
Exposing Berry/Pancharatnam phases in molecular adiabatic potential surface intersections
There are several ways to compute the Berry phase in molecules within the Born Oppenheimer framework. One way is through the "non-adiabatic coupling  matrix" defined by
matrix" defined by
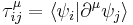
where 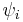 is the adiabatic electronic wave function, depending on the nuclear parameters
is the adiabatic electronic wave function, depending on the nuclear parameters 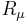 . The nonadiabatic coupling can be used to define a loop integral, analogous to the a Wigner loop (1974) in field theory, developed independently for molecular framework by M. Baer (1975, 1980, 2000). Given a closed loop
. The nonadiabatic coupling can be used to define a loop integral, analogous to the a Wigner loop (1974) in field theory, developed independently for molecular framework by M. Baer (1975, 1980, 2000). Given a closed loop 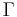 , parameterized by
, parameterized by 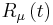 where
where ![t\in \left[ 0,1 \right]](/2012-wikipedia_en_all_nopic_01_2012/I/5b94b736d341f526833b46e4f0e21ccc.png) is a parameter and
is a parameter and 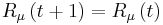 . The D-matrix is given by:
. The D-matrix is given by:
![D\left[ \Gamma \right]=\hat{P}e^{\oint_{\Gamma }{\tau ^{\mu }dR_{\mu }}}](/2012-wikipedia_en_all_nopic_01_2012/I/dd3da31a5a91b3b30b4f577bcf2c505a.png)
(here, 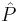 is a path ordering symbol). It can be shown that once
is a path ordering symbol). It can be shown that once  is large enough (i.e. a sufficient number of electronic states is considered) this matrix is diagonal with the diagonal elements equal to
is large enough (i.e. a sufficient number of electronic states is considered) this matrix is diagonal with the diagonal elements equal to 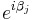 where
where 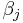 are the Berry phases associated with the loop for the
are the Berry phases associated with the loop for the  adiabatic electronic state.
adiabatic electronic state.
For time-reversal symmetrical electronic Hamiltonians the Berry phase reflects the number of conical intersections encircled by the loop. More accurately:
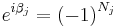
where 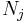 is the number of conical intersections involving the adiabatic state
is the number of conical intersections involving the adiabatic state 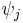 encircled by the loop
encircled by the loop 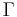 .
.
An alternative to the D-matrix approach would be a direct calculation of the Pancharatnam phase. This is especially useful if one is interested only in the Berry phases of a single adiabatic state. In this approach, one takes a number 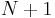 of points
of points 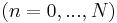 along the loop
along the loop 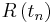 with
with 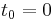 and
and 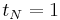 then using only the jth adiabatic states
then using only the jth adiabatic states ![\psi _{j}\left[ R\left( t_{n} \right) \right]](/2012-wikipedia_en_all_nopic_01_2012/I/1b4a82fa9391619a2a27dec2c11e3f18.png) computes the Pancharatnam product of overlaps:
computes the Pancharatnam product of overlaps:
![I_{j}\left( \Gamma ,N \right)=\prod\limits_{n=0}^{N-1}{\left\langle \psi _{j}\left[ R\left( t_{n} \right) \right] | \psi _{j}\left[ R\left( t_{n%2B1} \right) \right] \right\rangle }](/2012-wikipedia_en_all_nopic_01_2012/I/295e1aa2eb39f34c56b13bddefabae18.png)
In the limit 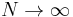 one has (See Ryb & Baer 2004 for explanation and some applications):
one has (See Ryb & Baer 2004 for explanation and some applications):
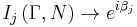
See also
- For the connection to mathematics, see curvature tensor,
- Aharonov–Bohm effect,
- Conical intersections of potential energy surfaces.
- Chern class
- Wilson loop
- Winding number
- Hannay angle
Notes
- ^ S. Pancharatnam (1956). "Generalized Theory of Interference, and Its Applications. Part I. Coherent Pencils". Proc. Indian Acad. Sci. A 44: 247–262.
- ^ M. V. Berry (1984). "Quantal Phase Factors Accompanying Adiabatic Changes". Proc. R. Soc. Lond. A 392 (1802): 45–57. Bibcode 1984RSPSA.392...45B. doi:10.1098/rspa.1984.0023.
- ^ Jens von Bergmann and HsingChi von Bergmann (2007). "Foucault pendulum through basic geometry". Am. J. Phys. 75 (10): 888–892. Bibcode 2007AmJPh..75..888V. doi:10.1119/1.2757623.
- ^ N. A. Sinitsyn and I. Nemenman (2007). "The Berry phase and the pump flux in stochastic chemical kinetics". Euro. Phys. Lett. 77 (5): 58001. arXiv:q-bio/0612018. Bibcode 2007EL.....7758001S. doi:10.1209/0295-5075/77/58001.
References
- Jeeva Anandan, Joy Christian and Kazimir Wanelik (1997). "Resource Letter GPP-1: Geometric Phases in Physics". Am. J. Phys. 65 (3): 180. arXiv:quant-ph/9702011. Bibcode 1997AmJPh..65..180A. doi:10.1119/1.18570.
- V. Cantoni and L. Mistrangioli (1992) "Three-Point Phase, Symplectic Measure and Berry Phase", International Journal of Theoretical Physics vol. 31 p. 937.
- Richard Montgomery, A Tour of Subriemannian Geometries, Their Geodesics and Applications (Mathematical Surveys and Monographs, Volume 91), (2002) American Mathematical Society, ISBN 0-8218-1391-9. (See chapter 13 for a mathematical treatment)
- Connections to other physical phenomena (such as the Jahn–Teller effect) are discussed here: [1]
- Paper by Prof. Galvez at Colgate University, describing Geometric Phase in Optics: [2]
- Surya Ganguli, Fibre Bundles and Gauge Theories in Classical Physics: A Unified Description of Falling Cats, Magnetic Monopoles and Berry's Phase [3]
- Robert Batterman, Falling Cats, Parallel Parking, and Polarized Light [4]
- M. Baer, "Adiabatic and diabatic representations for atom-molecule collisions: treatment of the collinear arrangement", Chem. Phys. Lett. 35, 112 (1975); M. Baer, "Electronic non-adiabatic transitions: Derivation of the general adiabatic-diabatic transformation matrix", Mol. Phys. 40, 1011 (1980); M. Baer, "Existence of diabetic potentials and the quantization of the nonadiabatic matrix", J. Phys. Chem. A 104, 3181-3184 (2000).
- I. Ryb and R. Baer, "Combinatorial invariants and covariants as tools for conical intersections", J. Chem. Phys. 121, 10370-10375 (2004). R. Baer, "Born-Oppenheimer invariants along nuclear paths", J. Chem. Phys. 117, 7405 (2002).
- Frank Wilczek and Alfred Shapere, "Geometric Phases in Physics", World Scientific, 1989
- Jerrold E. Marsden, Richard Montgomery, Tudor S. Ratiu (1990). Reduction, Symmetry, and Phases in Mechanics. AMS Bookstore. p. 69. ISBN 0821824988. http://books.google.com/?id=s7vcui7zUL0C&pg=PA69&dq=%22Berry+connection%22.
- C. Pisani (1994). Quantum-mechanical Ab-initio Calculation of the Properties of Crystalline Materials (Proceedings of the IV School of Computational Chemistry of the Italian Chemical Society ed.). Springer. p. 282. ISBN 3540616454. http://books.google.com/?id=5ak5TwSLreAC&pg=PA282&dq=%22Berry+connection%22.
- L. Mangiarotti, Gennadiĭ Aleksandrovich Sardanashvili (1998). Gauge Mechanics. World Scientific. p. 281. ISBN 9810236034. http://books.google.com/?id=-N6F44hlnhgC&pg=PA281&dq=%22Berry+connection%22.
- Karin M Rabe, Jean-Marc Triscone, Charles H Ahn (2007). Physics of Ferroelectrics a Modern Perspective. Springer. p. 43. ISBN 3540345906. http://books.google.com/?id=CWTzxRCDJdMC&pg=PA43&dq=%22Berry+connection%22.
- Michael Baer (2006). Beyond Born Oppenheimer. Wiley. ISBN 0471778915. http://books.google.com/?id=K8XKybgdDGgC&lpg=PP1&dq=Beyond%20Born%20Oppenheimer&pg=PP1#v=onepage&q&f=false.